Lenovo ThinkPad Yoga 12 - Wacom Active Pen or Wacom Digitizer Pen

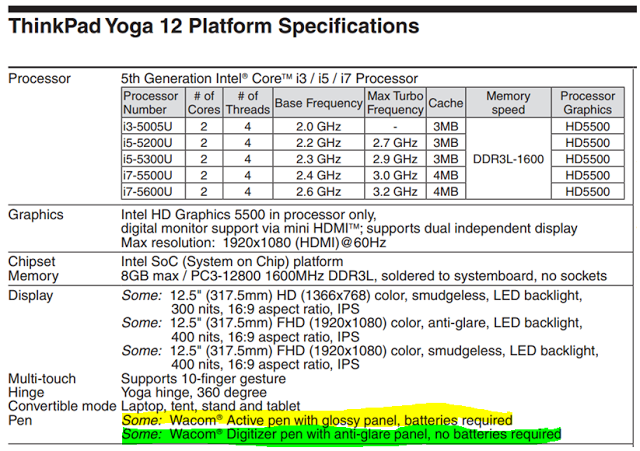
There are several digitizer options for the Lenovo ThinkPad Yoga 12.  Below you can find some information about the two options.

The Yoga 12 units that have a glossy panel, according to some documents by Lenovo, are compatible with the Wacom Active Pen. This Wacom technology is more recent and goes by the name of Active Eletro Static (Active ES), and does use batteries.  I have NOT yet tested a Yoga 12 unit with Active ES, so my assumption of compatibility is based on the Lenovo document.

The anti-glare version of the Yoga 12, according to the same Lenovo document, is compatible with the Lenovo ThinkPad Yoga Digitizer (4X80F22110).  This pen uses Wacom Penabled technology and does not require batteries.  I have used this technology with a Yoga 12 and know it works fine.

It is important to note that both of these pens are NOT compatible.  Therefore, if you use an Active Pen on a Penabled device (like the ThinkPad X230T) the device will not respond to the Active Pen.  Likewise, if you use a Penabled pen on an Active ES device (like a Toshiba Encore 2 tablet) the device will not react to the pen.

There may be models of the Yoga 12 that do NOT support digitizer pen.  So just because you have a certain screen version does not guarantee that either of the pens will work.  But, at least knowing the screen version may increase your chances of getting the pen option that you want.

Which one is better?  I have mostly used Penabled devices, but my experience with a Toshiba Encore 2 tablet that uses Active ES was very pleasant.  So as of right now I have to say that either of them is fine.

Note: Both of these pen technologies seem to be better than N-Trig DuoSense 2 (as seen in the Microsoft Surface Pro 3 tablet).

List of Keyboard Shortcuts

These are keyboard shortcuts in Windows. 

Text Editor (test with Notepad++)

Key Combination : What it does.
Home : move to beginning of line.
End : move to the end of line.
Pg Up or Pg Down : moves the cursor up or down one "screen" at a time.;
Shift + Home : selects text left of cursor to the end of the line.
Shift + End : selects text right of cursor to the end of the line.
Shift + (Left or Right) : selects  one character at a time.
Shift + Up : selects text from current position all the way to above the cursor.
Shift + Down : selects text from current position all the way to below the cursor.
Ctrl + A : selects all text.
Ctrl + C : copy text.
Ctrl + V : paste text.
Ctrl + X : cut text.
Ctrl + Z : undo.
Ctrl + Y : redo.
Ctrl + N : new document.
Ctrl + S : save document.
Ctrl + O : open document.
Ctrl + P : print.
Ctrl + (Left or Right) : moves the cursor left or right one word at a time.
Ctrl + Shift + (Left or Right) : moves and selects text one word at a time.
Ctrl + Shift + (Up or Down) : move the current text line up or down.
Ctrl + W : closes the current tab or window
Alt + (a alphanumeric key) : opens the menu item who's label text starts with the alphanumeric key.

Windows
Win + (Left or Right) : place the window left or right.
Win + Up : maximize window.
Win + Down : restore window, then minimize window.
Alt + Tab : switch window (note that holding tab key keeps the preview windows open, releasing tab closes the preview window).
Ctrl + Alt + Tab : switch window and keep it open until a selection occurs.

Boogie Board Sync 9.7 - Box Contents & Details

The Boogie Board Sync 9.7 is an electronic "eWriter."  From my side it looks like two devices in one.  It seems to have stylus-only features but at the same time has more advanced features found in digitizer devices.  More info below.